整数拆分

发表于
本文字数： 1.8k 阅读时长 ≈ 2 分钟

LeetCode每日一题，343. Integer Break

先看题目描述

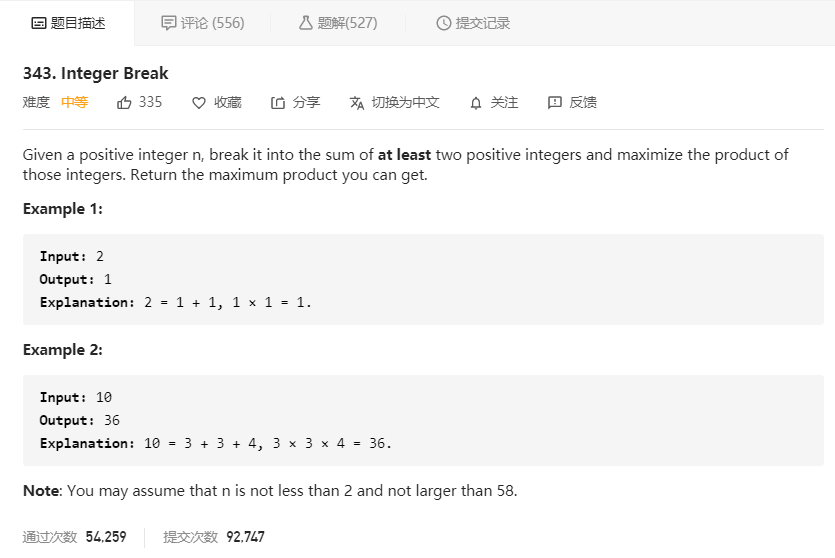
大意就是给定一个整数 n，将其拆分成至少两个正整数，并将拆分出的正整数相乘，返回乘积的最大值

算法和思路

动态规划

  • 数组 dp[i] 表示将 i 拆分成至少两个正整数的和后，这些正整数的最大乘积

  • 当 i ≥ 2 时，假设对正整数 i 拆分出的第一个正整数是 j（2 <= j <= i / 2），则有以下两种方案：

    • 将 i 拆分成 j 和 i - j 的和，且 i - j 不再拆分，此时乘积为 j * (i - j)
    • 将 i 拆分成 j 和 i - j 的和，且 i - j 再拆分，此时最大乘积为 j * dp[i - j]

  • 因此，当 j 固定时，有 dp[i] = max(j * (i - j), j * dp[i - j])，其中 j 从 2 遍历到 i / 2，dp[i] 取其中最大值

  • 最终返回 dp[n]

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            int cur = 0;
            for (int j = 1; j <= i / 2; j++) {
                cur = Math.max(cur, j * Math.max(dp[i - j], i - j));
            }
            dp[i] = cur;
        }
        return dp[n];
    }
}

后来看题解才知道还有时间复杂度为 O(n) 的优化后的动态规划法和时间复杂度为 O(1) 的数学法，但因为涉及到数学推导和证明，当时并没有想到，题解也没太看懂，还是把另外两种方法的实现代码贴上来一下吧

优化后的动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int integerBreak(int n) {
        if (n < 4) {
            return n - 1;
        }
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            dp[i] = Math.max(Math.max(2 * (i - 2), 2 * dp[i - 2]), Math.max(3 * (i - 3), 3 * dp[i - 3]));
        }
        return dp[n];
    }
}

数学

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int integerBreak(int n) {
        if (n <= 3) {
            return n - 1;
        }
        int quotient = n / 3;
        int remainder = n % 3;
        if (remainder == 0) {
            return (int) Math.pow(3, quotient);
        } else if (remainder == 1) {
            return (int) Math.pow(3, quotient - 1) * 4;
        } else {
            return (int) Math.pow(3, quotient) * 2;
        }
    }
}