分割数组的最大值

发表于
本文字数： 2.7k 阅读时长 ≈ 2 分钟

LeetCode每日一题，410. Split Array Largest Num

先看题目描述

大意是给定一个非负整数数组和一个整数 m ，将这个数组分成连续的子数组，求出子数组和的最大值中的最小值

算法和思路

看了题解才知道该用动态规划或二分法

动态规划

  • dp[i][j] 表示将数组中前 i 个数分成 j 段后所能得到的最大连续子数组和的最小值
  • 状态转移方程：
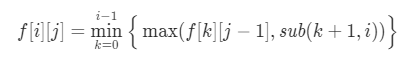
  • 对于状态 dp[i][j]，由于我们不能分出空的子数组，因此合法的状态必须有 i ≥ j。对于不合法 (i < j) 的状态，由于我们的目标是求出最小值，因此可以将这些状态全部初始化为一个很大的数。在上述的状态转移方程中，一旦我们尝试从不合法的状态 dp[k][j - 1] 进行转移，那么 max(⋯) 将会是一个很大的数，就不会对最外层的 min{⋯} 产生任何影响
  • 在上述的状态转移方程中，当 j = 1 时，唯一的可能性就是前 i 个数被分成了一段，如果枚举的是 k = 0，那就代表这种情况；如果 k != 0，那对应的状态 dp[k][0] 就是不合法的情况，无法进行转移，因此仅令 dp[0][0] = 0

二分查找 + 贪心

「使……最大值尽可能小」是二分搜索题目常见的问法。

由题意可知：子数组的最大值是有范围的，即在区间 [max(nums), sum(nums)] 之中。

本题中，我们注意到：当我们选定一个值 x，我们可以线性地验证是否存在一种分割方案，满足其最大分割子数组和不超过 x。策略如下：

贪心地模拟分割的过程，从前到后遍历数组，用 sum 表示当前分割子数组的和，cnt 表示已经分割出的子数组的数量（包括当前子数组），那么每当 sum 加上当前值超过了 x，我们就把当前取的值作为新的一段分割子数组的开头，并将 cnt 加 1。遍历结束后验证是否 cnt 不超过 m，cnt 表示的就是数组和的最大值不大于 mid 对应的子数组个数。如果 cnt > m，说明划分的子数组多了，即我们找到的 mid 偏小，故令 l = mid + 1；否则，说明划分的子数组少了，即 mid 偏大(或者恰好等于目标值)，故令 h = mid

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.Arrays;

class Solution {
    public int splitArray(int[] nums, int m) {
        int n = nums.length;
        int[][] dp = new int[n + 1][m + 1];
        int[] sub = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        for (int i = 1; i <= n; i++) {
            sub[i] = sub[i - 1] + nums[i - 1];
        }
        dp[0][0] = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= Math.min(i, m); j++) {
                for (int k = 0; k < i; k++) {
                    dp[i][j] = Math.min(dp[i][j], Math.max(dp[k][j - 1], sub[i] - sub[k]));
                }
            }
        }
        return dp[n][m];
    }
}

二分查找 + 贪心

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public int splitArray(int[] nums, int m) {
        int left = 0, right = 0;
        for (int i = 0; i < nums.length; i++) {
            right += nums[i];
            if (left < nums[i]) {
                left = nums[i];
            }
        }
        while (left < right) {
            int mid = (right - left) / 2 + left;
            if (check(nums, mid, m)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

    public boolean check(int[] nums, int x, int m) {
        int sum = 0;
        int cnt = 1;
        for (int i = 0; i < nums.length; i++) {
            if (sum + nums[i] > x) {
                cnt++;
                sum = nums[i];
            } else {
                sum += nums[i];
            }
        }
        return cnt <= m;
    }
}