不同的二叉搜索树

发表于
本文字数： 1.3k 阅读时长 ≈ 1 分钟

LeetCode每日一题，96. Unique Binary Search Trees

先看题目描述

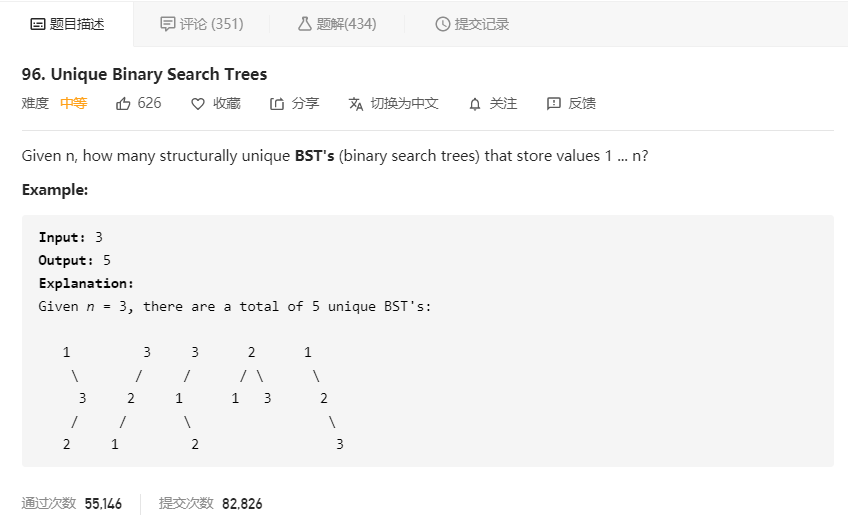
大意就是给定二叉树的节点数量，问有多少种不同结构的二叉树

算法和思路

大致思路就是有 n 个节点的二叉树，那么其左子树的节点数为 0 到 n - 1，右子树的相应节点数为 n - 1 到 0，那么每次将左子树可能的结构数量与右子树可能的结构数量相乘，最后累加即可

动态规划

  • dp[i] 表示有 i 个节点的二叉树共有多少种结构
  • 初始化时 dp[0] = 1，dp[1] = 1
  • 状态转移方程：dp[i] = dp[0] * dp[i - 1] + dp[1] * dp[i - 2] + … + dp[i - 2] * dp[1]] + dp[i - 1] * dp[0]
  • 最后返回 dp[n] 即可

算法源码

一开始是用递归实现的，运行效率十分感人

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int numTrees(int n) {
        if (n == 0) return 1;
        if (n == 1) return 1;
        int res = 0;
        if (n % 2 == 1) {
            for (int i = 0; i < n / 2; i++) {
                res += numTrees(i) * numTrees(n - 1 - i) * 2;
            }
            res += numTrees(n / 2) * numTrees(n / 2);
        } else {
            for (int i = 0; i < n / 2; i++) {
                res += numTrees(i) * numTrees(n - 1 - i) * 2;
            }
        }
        return res;
    }
}

看了题解后改成用动态规划，运行效率就大大提高了

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - 1 -j];
            }
        }
        return dp[n];
    }
}