三角形最小路径和

发表于
本文字数： 2k 阅读时长 ≈ 2 分钟

LeetCode每日一题，120. Triangle

先看题目描述

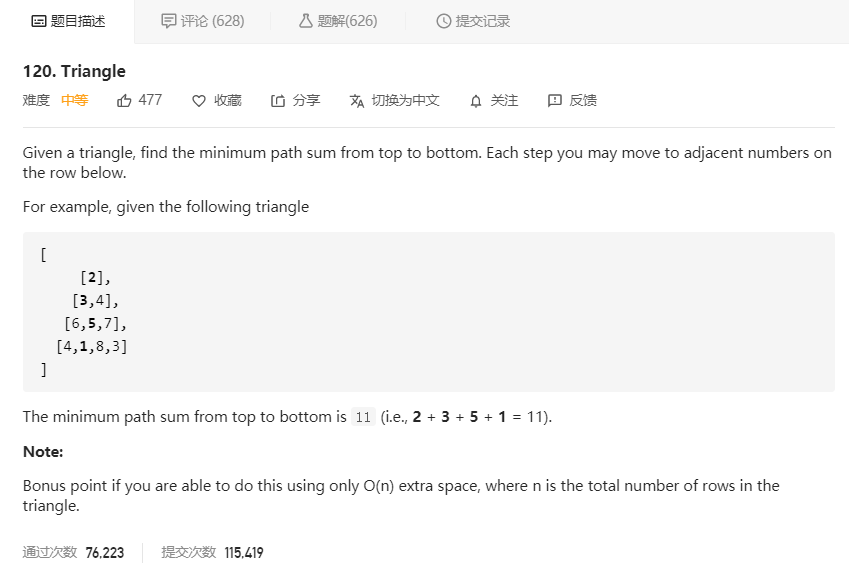
大意是给定一个三角形，返回从顶点到底部的最小路径和

算法和思路

第一反应是用递归，然后自己用递归实现以后去提交，发现时间超出限制，于是去看题解，发现这题用动态规划就可以

动态规划

  • dp[i][j] 表示从三角形顶点到第 i 行第 j 列的最小路径和
  • 状态转移方程：
    • 当 j = 0 时，dp[i][j] = dp[i - 1][0] + triangle[i][j]
    • 当 j = i 时，dp[i][j] = dp[i - 1][j - 1] + triangle[i][j]
    • 其他情况下，dp[i][j] = min(dp[i] - 1[j - 1], dp[i - 1][j] ) + triangle[i][j]
  • 最终返回 dp[len - 1][0] 至 dp[len - 1][len - 1] 中的最小值即可

空间优化

可以发现， dp[i][j] 只与 dp[i - 1][…] 有关，而与 dp[i - 2][…] 及之前的状态无关，因此我们不必存储这些无关的状态。具体地，我们使用两个长度为 n 的一维数组进行转移，将 i 根据奇偶性映射到其中一个一维数组，那么 i-1 就映射到了另一个一维数组，这样我们使用这两个一维数组，交替地进行状态转移，最后根据三角形高度的奇偶性来选择其中一个一维数组中的最小值并返回

算法源码

一开始递归实现的源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import java.util.*;

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        return minPath(triangle, 0, 0);
    }

    public int minPath(List<List<Integer>> triangle, int i, int j) {
        if (i == triangle.size() - 1) {
            return triangle.get(i).get(j);
        }
        return triangle.get(i).get(j) + Math.min(minPath(triangle, i + 1, j), minPath(triangle, i + 1, j + 1));
    }
}

看了题解后使用动态规划并空间优化后的源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.*;

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int len = triangle.size();
        int[][] dp = new int[2][len];
        dp[0][0] = triangle.get(0).get(0);
        for (int i = 1; i < len; i++) {
            int cur = i % 2;
            int prev = 1 - cur;
            dp[cur][0] = dp[prev][0] + triangle.get(i).get(0);
            for (int j = 1; j < i; j++) {
                dp[cur][j] = triangle.get(i).get(j) + Math.min(dp[prev][j - 1], dp[prev][j]);
            }
            dp[cur][i] = dp[prev][i - 1] + triangle.get(i).get(i);
        }
        int min = Integer.MAX_VALUE;
        int n = (len - 1) % 2;
        for (int i = 0; i < len; i++) {
            min = Math.min(min, dp[n][i]);
        }
        return min;
    }
}