LeetCode每日一题,309.Best Time to Buy and Sell Stock with Cooldown
先看题目描述
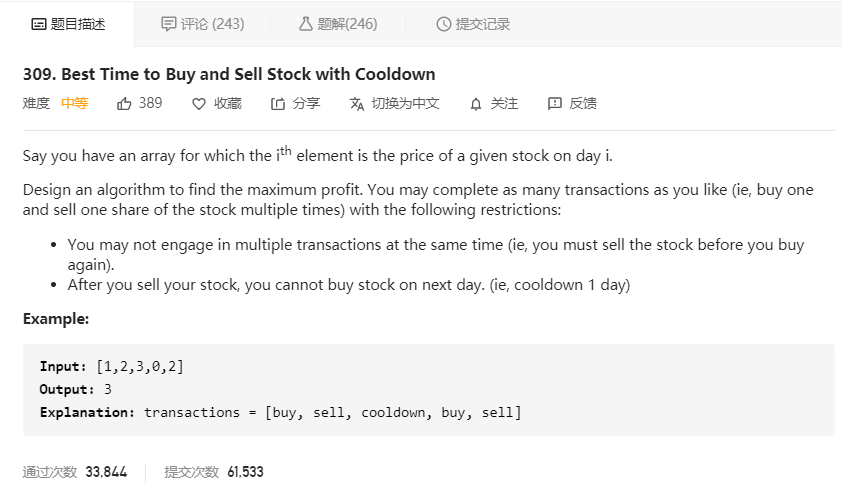
大意就是给定一个整型数组,第 i 项代表第 i 天的股票价格,让我们计算买卖股票的最大利润,其中有两个约束条件, 1:再次购买股票前要出售之前的股票;2:卖出股票后,有一天的冷冻期
算法和思路
第一反应是动态规划,想用 dp[i] 代表第 i 天累积的最大利润,但没想出状态转移方程,然后就去看题解,发现还要对一天可能的三种状态进行分析
我们用 dp[i] 表示第 i 天开始时的累计最大收益,根据题目描述,由于我们最多只能同时买入(持有)一支股票,并且卖出股票后有冷冻期的限制,因此我们会有三种不同的状态:
- 目前持有一支股票,对应的最大收益记为 dp[i][0]
- 目前不持有股票,且处于冷冻期中,对应的最大收益记为 dp[i][1
- 目前不持有股票,且不处于冷冻期中,对应的最大收益记为 dp[i][2]
下面就是如何分析状态转移方程,显而易见第 i 天的状态从第 i - 1 天的状态转移而来,接下来就是分析三种状态:
- dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - prices[i - 1]),因为第 i 天开始时持有股票,要么第 i -1 天开始时就持有股票,要么第 i - 1 天开始时不处于冷冻期然后买了一支股票
- dp[i][1] = dp[i - 1][0] + prices[i - 1],因为第 i 天开始时不持有股票且处于冷冻期,只有可能是第 i - 1 天开始时持有股票,然后将该股票出售
- dp[i][2] = max(dp[i - 1][1], dp[i - 1][2]),因为第 i 天开始时不持有股票且不处于冷冻期,要么是第 i - 1 天开始时不持有股票但处于冷冻期,要么是第 i - 1 天开始时就不持有股票且不处于冷冻期
最终返回 max(dp[len][1], dp[len][2]) 即可, 因为最后一天(第 len - 1 天)结束,第 len 天开始时,要想累计收益最大,显然是不会持有股票的
之后就是一些细节和初始化的问题,初始化时 dp[0][0] = -prices[0], dp[0][1] = 0,dp[0][2] = 0,实际上第 0 天开始时是不可能处于 dp[0][0] 和 dp[0][1],但为了计算仍对其初始化,同理第 1 天开始时也不可能处于 dp[1][1],但这并不影响每天累计最大收益的运算
实现源码
1 | class Solution { |
虽然这个代码通过了测试,但运行效率并不理想,因为使用的是数组,每个状态的结果都记录了下来,而且重复访问数组也增加了运行时间。为了改善运行的时间效率和空间效率,我们发现 dp[i][…] 只与 dp[i - 1][…] 有关,而与之前的所有状态无关,我们不必存储这些无关状态,因此我们只需要将 dp[i - 1][0], dp[i - 1][1], dp[i - 1][2] 存储在三个变量中,遍历过程中不断维护这三个变量,最终返回结果即可
下面是实现源码
1 | class Solution { |