最佳观光组合

发表于
本文字数： 1.9k 阅读时长 ≈ 2 分钟

LeetCode每日一题，1014.Best Sightseeing Pair

先看题目描述

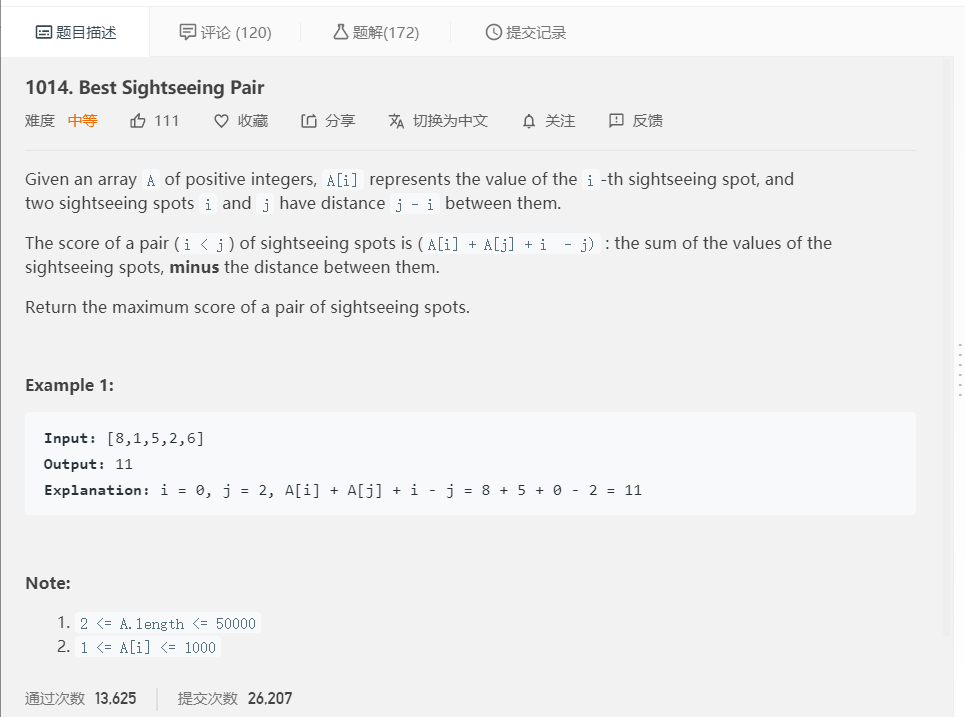
算法和思路

这道题遍历一遍 A 数组即可，关键是遍历到第 i 个元素时，要注意到 A[i] + i 是个定值，找到 A[j] - j 的最大值即可，这道题可正向遍历，也可反向遍历，正向遍历时把 A[j] - j 看作定值，遍历到景点 j 时，最大化 A[i] + i + A[j] - j 的值其实就等价于求 [0, j - 1] 中 A[i] + i 的最大值 max，景点 j 的答案即为 max + A[j] - j，在从前往后遍历的过程中一直维护 ans 和 max 的值即可；反向遍历时，把 A[i] + i 看成定值，遍历到景点 i 时，最大化 A[i] + i + A[j] - j 的值其实就等价于求 [i + 1, len - 1] 中 A[j] - j 的最大值 max，景点 i 的答案即为 A[i] + i + max，在从后往前遍历的过程中一直维护 ans 和 max 的值即可

但是我一开始做时，想的是把 A[i] + i 看成定值，但用的却是从前往后遍历，于是维护 max 的过程就很麻烦，最后超出了时间限制

算法源码

下面会给出三种源码，分别是一开始超出时间限制的源码，正向遍历源码和反向遍历源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.*;

class Solution {
    public int maxScoreSightseeingPair(int[] A) {
        int len = A.length;
        int max = 0;
        int[] B = new int[len];
        for (int i = 1; i < len; i++) {
            B[i] = A[i] - i;
        }
        List<Integer>  values = new LinkedList<>();
        for (int num: B) {
            values.add(num);
        }
        Collections.sort(values);
        for (int i = 0; i < len - 1; i++) {
            values.remove(values.indexOf(B[i]));
            int cur_max = A[i] + i + values.get(values.size()-1);
            max = Math.max(cur_max, max);
        }
        return max;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxScoreSightseeingPair(int[] A) {
        int len = A.length;
        int ans = 0;
        int max = A[0] + 0;
        for (int j = 1; j < len; j++) {
            ans = Math.max(ans, max + A[j] - j);
            max = Math.max(max, A[j] + j);
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxScoreSightseeingPair(int[] A) {
        int len = A.length;
        int ans = 0;
        int max = A[len - 1] - (len - 1);
        for (int i = len - 2; i >= 0; i--) {
            ans = Math.max(ans, A[i] + i + max);
            max = Math.max(max, A[i] - i);
        }
        return ans;
    }
}