柱状图中最大的矩形

发表于
本文字数： 2.9k 阅读时长 ≈ 3 分钟

LeetCode每日一题，84.Largest Rectangle in Histogram

先看题目描述

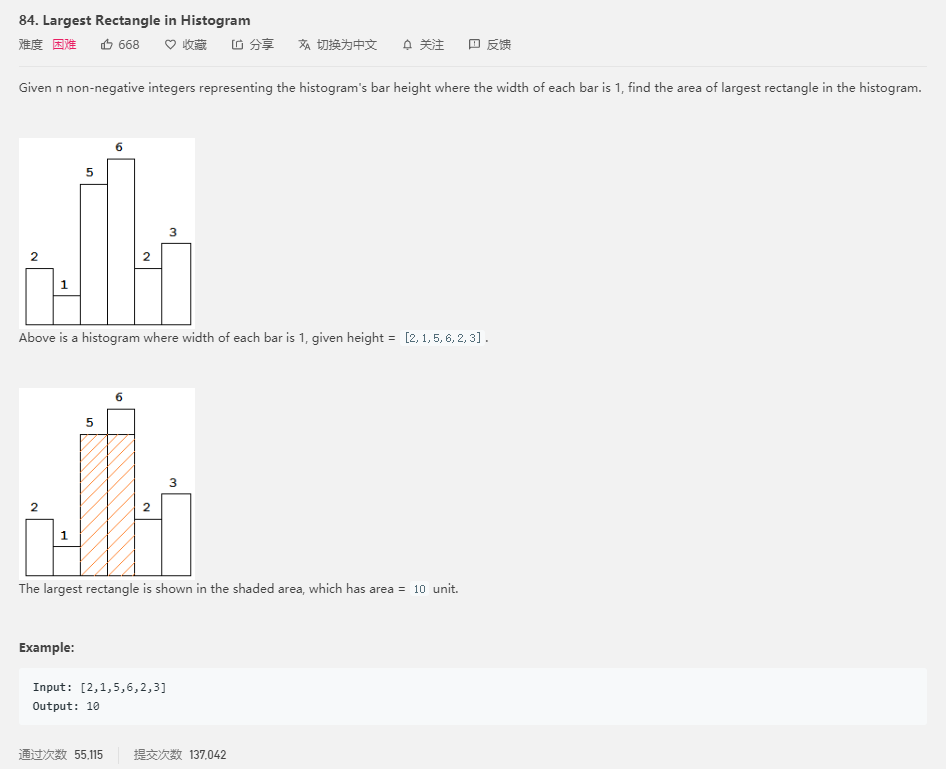
题目大意就是给出n个非负整数，代表柱形图中各个柱形的宽度，且柱形宽度为1，求在该柱形图中，能勾勒出的矩形的最大面积

算法和思路

最开始想到的是暴力求解法，就是遍历数组中每个数，以每个柱形的高度作为矩形高度，然后向两边扩散，直至不能扩散为止，求出矩形宽度，从而求出矩形的面积，最终取各矩形中的面积最大值返回，下面是实现源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import java.util.*;

class Solution {
    public int largestRectangleArea(int[] heights) {
        int max = 0;
        for (int i = 0; i < heights.length; i++) {
            int left = i;
            int right = i;
            while(left >= 0 && heights[left] >= heights[i]) {
                left--;
            }
            while (right < heights.length && heights[right] >= heights[i]) {
                right++;
            }
            if ((heights[i] * (right - left - 1)) > max) max = heights[i] * (right - left - 1);
        }
        return max;
    }
}

虽然代码通过了检验，但时间和空间上的效率都不怎么样，时间复杂度为O(N2)，空间复杂度为O(1)，之后看了题解才知道怎么优化，优化思路是以空间换时间，在遍历的过程中用栈来记录一些信息，使得可以一次遍历，不需要中心扩散就能够计算出每一个高度所对应的最大面积的矩形的面积

单调栈法

算法流程

  • 遍历heights数组，当遍历到第 i 个元素时

  • 若栈为空，则将 i 直接入栈

  • 若栈不为空，比较栈顶元素对应的高度 height 与 heights[i]

    • 若 heights[i] >= height，将 i 入栈
    • 若 heights[i] < height，将栈顶元素出栈，则此时 height 所对应的最大面积矩形的面积可以计算
      • 若此时栈为空，则矩形宽度为 i，计算面积并更新 max
      • 若此时栈不为空，则矩形宽度为 i - 栈顶元素 - 1，计算面积并更新 max

  • 重复上一步直到 heights[i] >= height 或 栈为空，将 i 入栈

  • heights 数组遍历完后，栈内必定还有元素，则将栈顶元素依次出栈，计算对应矩形的面积并更新 max，计算方法和上面相同，不过是将 i 换为数组长度

  • 返回 max

可以看到我们在缓存数据时，是从左向右缓存的，我们计算出一个结果的顺序是从右向左，并且计算完成以后就不再需要，符合后进先出的特点，故使用的数据结构为栈

还有一个需要注意的细节是我们在计算矩形面积时，除了右边要比当前严格小，其实左边也需要比当前严格小，但在代码中只体现了右边严格小于当前，没体现左边严格小于当前，那么如果左边的高度和当前高度相等，会不会有影响呢？答案是对于该高度对应的部分矩形，计算面积会有错误，但最后仍能得到正确的面积，不会影响最终结果。因为对于一串重复高度中的第一个，我们计算出来的面积会是正确的

以 [5, 2, 5, 5]为例，此时出栈顺序为 0, 3, 2, 1，当 0 出栈时，得到面积为 5；当 3 出栈时，得到面积为 5；当 2 出栈时，得到面积为 10；当 1 出栈时，得到面积为 8。可以看到对于高度为 5 的矩形，我们最后仍可以计算出对应的最大面积为 10，不会影响最终结果

下面是实现源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.*;

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        if (len == 0) return 0;
        if (len == 1) return heights[0];
        int max = 0;
        Deque<Integer> stack = new ArrayDeque<>(len);
        for (int i = 0;i < len; i++) {
            while(!stack.isEmpty() && heights[stack.peek()] > heights[i]) {
                int height = heights[stack.pop()];
                if(!stack.isEmpty()) {
                    int left = stack.peek();
                    max = Math.max(max, height * (i - left -1));
                } else {
                    max = Math.max(max, height * i);
                }
            }
            stack.push(i);
        }
        while(!stack.isEmpty()) {
            int height = heights[stack.pop()];
            if(!stack.isEmpty()) {
                int left = stack.peek();
                max = Math.max(max, height * (len - left -1));
            } else {
                max = Math.max(max, height * len);
            }
        }
        return max;
    }
}